Pythonで学ぶアルゴリズム入門:仕組み、必要性、実例とその応用
2024年11月26日

こんにちは!
今回の記事では、アルゴリズムについて解説します。突然ですが、「アルゴリズム」という言葉を聞いたことはありますか?
プログラミングを学び始めると、この言葉が頻繁に登場しますが、最初は少し難しそうに感じるかもしれません。実際のところ、アルゴリズムは私たちの日常生活にも深く関わっています。
例えば、料理のレシピや通勤経路の選択など、目的を達成するための手順はすべてアルゴリズムの一種と考えることができます。
本記事では、「アルゴリズムとは何か」という基本的な部分から、Pythonを使った具体的な実装例まで丁寧に解説していきます。
これを読み終える頃には、アルゴリズムの理解が深まり、プログラミングスキルを一段と高める一歩を踏み出せるはずです。それでは始めましょう!
アルゴリズムとは何か?
プログラミングを学ぶ中で、「アルゴリズム」という言葉を耳にする機会が多いと思います。では、アルゴリズムとは一体何でしょうか?
簡単に言えば、「特定の目的を達成するための一連の手順」です。
例えば、料理のレシピもアルゴリズムの一例と言えます。「材料を揃える」「順番に炒める」といったステップがレシピの指示であり、結果として美味しい料理が出来上がります。
プログラミングにおいて、アルゴリズムは計算やデータ処理、問題解決の鍵となります。例えば、リストの中から最大の数字を探す、最短経路を計算する、データを効率よく並べ替える、こうした処理はすべてアルゴリズムによって実現されます。
なぜアルゴリズムを学ぶ必要があるのか?
なぜアルゴリズムを学ぶ必要があるのでしょうか?
そもそも、プログラミングは単にコードを書くことが目的ではありません。
その背後には、効率的なリソースの利用、迅速な計算処理、そして問題を分解して解決するスキルが求められます。そのためには、アルゴリズムを理解する必要があります。
アルゴリズムを学ぶと以下のようなメリットがあります。
問題解決の土台となる
プログラミングにおける課題は、単に動くコードを書くことに留まりません。
膨大なデータを扱うとき、非効率な方法では処理に時間がかかりすぎることもあります。アルゴリズムを学ぶことで、問題の構造を理解し、最適な解決方法を考えるスキルが身につきます。
処理の効率化を可能にする
プログラムの実行速度は、選択するアルゴリズムによって大きく変わります。例えば、データの検索や並べ替えなど日常的なタスクでも、適切なアルゴリズムを用いれば処理速度が飛躍的に向上します。
「線形探索はシンプルだが遅い」「二分探索はデータがソートされていればより速い」
といったように、効率を意識した選択ができるようになります。
このような理由からアルゴリズムを理解する必要があります。次は、具体的にPythonを使ってアルゴリズムを学んでみましょう。
【関連】Python中級者レベルになるためには?〜プログラミング初心者の脱却
Pythonでアルゴリズムを実装する実例
Pythonはアルゴリズムを学ぶのに非常に適した言語です。その理由は、コードが読みやすく、構文が簡単だからです。また、リストや辞書といった豊富なデータ型やライブラリが標準で用意されているため、基本的なアルゴリズムの実装がスムーズに行えます。
以下では、アルゴリズムを学びながらPythonでの実装を体験できるように、具体例を3つ紹介します。それぞれのアルゴリズムにはメリット・デメリットがあり、用途に応じて選択が重要です。
線形探索 (Linear Search)
まず最初に取り上げるのは「線形探索」です。
このアルゴリズムは、リスト内のデータを1つずつ順番に調べていき、目的の値を探すという非常にシンプルな方法です。例えば、教科書の中で特定の単語を見つける作業を想像してみてください。1ページずつ順番に読み進めるようなものです。
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i # 値が見つかったらそのインデックスを返す
return -1 # 見つからなかった場合この関数は、リストの各要素を1つずつチェックし、目標となる値が見つかればそのインデックスを返します。
もしリストを最後まで調べても見つからなければ -1 を返します。例えば、以下のコードを実行してみてください。
numbers = [3, 8, 2, 5, 9]
result = linear_search(numbers, 5)
print("結果:", result) # 出力: 結果: 3線形探索の最大の利点は、そのシンプルさにあります。特別な準備やデータの並び替えが不要で、どんなデータにも適用可能です。
ただし、大量のデータを扱う場合、全要素を順番に調べるため効率が悪く、処理時間が増えるという欠点もあります。
二分探索 (Binary Search)
次に紹介するのは「二分探索」です。
このアルゴリズムは、データがあらかじめソートされている場合に適用できる非常に効率的な探索方法です。リストを半分に分割しながら目標値を探すため、探索回数を大幅に減らすことができます。
例えば、図書館で本を探す場面を考えてみてください。ジャンルや作者名順に整理された棚から本を探すとき、初めから順番に調べるのではなく、目星をつけて範囲を絞り込むでしょう。それが二分探索の考え方です。
以下はPythonでの二分探索の実装例です。
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1このコードでは、リストの中央要素と目標値を比較し、中央値より小さいか大きいかによって探索範囲を左右どちらかに絞り込みます。
例えば、次のように使えます。
numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9]
result = binary_search(numbers, 4)
print("結果:", result) # 出力: 結果: 3この例では、ソートされたリスト [1, 2, 3, 4, 5, 6, 7, 8, 9] から値 4 を探し、そのインデックス 3 を返します。
二分探索の強みはその効率性にあります。
検索範囲を半分ずつ減らしていくため、大量のデータを高速に処理できます。ただし、データが未ソートの場合は適用できないという制約があり、事前にデータをソートする手間がかかる点が注意すべきポイントです。
バブルソート (Bubble Sort)
最後に紹介するのは「バブルソート」です。
このアルゴリズムは、隣り合う要素を比較しながらデータを並び替える方法です。小さな値が泡のように上がっていくイメージから「バブルソート」と名付けられました。
例えば、テストの点数を低い順に並び替えたい場合、このアルゴリズムを使うと簡単に実現できます。以下はPythonでの実装例です。
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]次のコードで試してみましょう。
numbers = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(numbers)
print("ソート後:", numbers) # 出力: ソート後: [11, 12, 22, 25, 34, 64, 90]このコードでは、リストの中の隣り合う要素を順に比較し、大きい方を右に、小さい方を左に移動させることでデータを昇順に並べ替えます。
バブルソートは初心者でも理解しやすく、簡単に実装できる点がメリットです。
しかし、全てのデータを繰り返し比較するため、大規模なデータセットでは非常に非効率です。計算量が O(n^2) であるため、実際のプロジェクトで使用されることは少なく、学習目的が主な用途となります。
アルゴリズム一覧
上記以外にも、さまざまなアルゴリズムがあります。
アルゴリズムには、以下のようなものがあります。
| アルゴリズム名 | 特徴 | 説明 |
|---|---|---|
| 線形探索 (Linear Search) | シンプルで直感的、ソート不要 | リストの先頭から順番に要素を調べていき、目的の値を見つける。データが未ソートでも適用可能だが、大規模なデータでは非効率。計算量は O(n)。 |
| 二分探索 (Binary Search) | 高速で効率的、ソート済みデータが必要 | リストを半分に分割しながら目標値を探す。探索回数が大幅に削減されるが、データがソートされている必要がある。計算量は O(log n)。 |
| バブルソート (Bubble Sort) | シンプルなソートアルゴリズム | 隣り合う要素を比較しながら並び替える。学習目的に適しているが、大規模なデータでは非効率。計算量は O(n^2)。 |
| クイックソート (Quick Sort) | 高速で実用的なソートアルゴリズム | ピボットを選び、それより小さい値を左、大きい値を右に分ける分割統治法を用いる。平均計算量は O(n log n) だが、最悪の場合 O(n^2)。 |
| マージソート (Merge Sort) | 安定ソート、分割統治法 | リストを再帰的に分割し、部分的にソートしてから結合する。安定性があり、大規模データでも効率的。計算量は O(n log n)。 |
| ダイクストラ法 (Dijkstra’s Algorithm) | グラフアルゴリズム、最短経路を求める | 重み付きグラフにおいて、1つの始点から他の全ての点への最短経路を計算する。計算量は O(V^2) またはヒープを用いると O(E + V log V)(V:頂点数, E:辺数)。 |
| 深さ優先探索 (DFS) | グラフ探索、スタックまたは再帰を使用 | グラフやツリー構造を深く進み、行き止まりに到達したらバックトラックする探索法。特定の構造の発見や経路探索に向いている。計算量は O(V + E)。 |
| 幅優先探索 (BFS) | グラフ探索、キューを使用 | グラフやツリー構造を浅い部分から広く探索する方法。最短経路問題にも適用可能。計算量は O(V + E)。 |
| 動的計画法 (Dynamic Programming, DP) | 最適部分構造、計算の重複を解消 | 問題を小さな部分問題に分割し、それを再利用することで効率的に解を導く手法。フィボナッチ数列やナップサック問題などに適用。計算量は問題に応じて異なる。 |
| 貪欲法 (Greedy Algorithm) | 局所的な最適解を選択し続ける | 問題を解くためにその場で最良と見える選択を繰り返す手法。ただし、必ずしも全体最適解を保証するわけではない。ハフマン符号や最小全域木の構築などに適用。 |
| クラスカル法 (Kruskal’s Algorithm) | グラフアルゴリズム、最小全域木を構築 | グラフの辺をコスト順にソートし、サイクルを形成しないように最小全域木を構築するアルゴリズム。計算量は O(E log E)。 |
| プリム法 (Prim’s Algorithm) | グラフアルゴリズム、最小全域木を構築 | 任意の始点から出発し、コストの最小な辺を順に追加して最小全域木を構築する。計算量は O(V^2) または O(E + V log V)(ヒープを使用)。 |
| ヒープソート (Heap Sort) | ヒープ構造を使用した効率的なソート | 最大ヒープまたは最小ヒープを構築し、要素を取り出しながら並び替える。計算量は O(n log n)。 |
| フロイド–ワーシャル法 (Floyd-Warshall Algorithm) | グラフアルゴリズム、全点間の最短経路 | 全ての頂点ペア間の最短経路を効率的に計算する動的計画法ベースのアルゴリズム。計算量は O(V^3)。 |
Pythonでアルゴリズムを学ぶためにおすすめのサイト
Pythonでアルゴリズムを学んでみたい方は、「Python WebAcademy」をお試しください。
以下のように、アルゴリズムの解説とブラウザ上でPythonを実行できる環境があります。ハンズオンで学習を進めることができるため、理解が深まります。
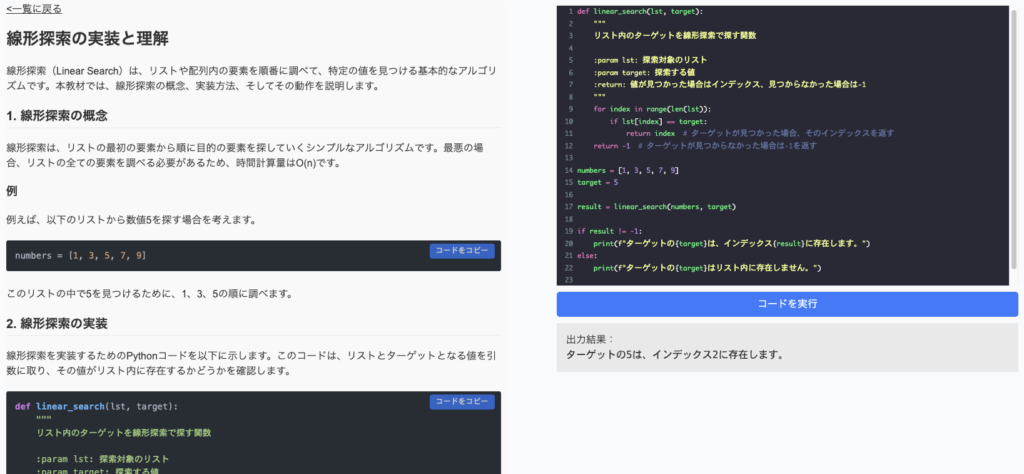
このサイトでは、さまざまなアルゴリズムをPythonで実装しながら学ぶことができます。アルゴリズムを学んでみたいと思う方は是非お試しください。
まとめ
ここまで、アルゴリズムの基本的な考え方からPythonでの具体的な実装例までを解説してきました。
アルゴリズムを学ぶことで、プログラムの効率化や問題解決のスキルが向上し、より高度なプロジェクトにも挑戦できるようになります。また、アルゴリズムはプログラミング初心者だけでなく、経験豊富なエンジニアにとっても重要な技術です。
最初は少し難しく感じるかもしれませんが、実際に手を動かしてコードを書きながら学ぶことで、次第にその仕組みがわかるようになります。
この記事をきっかけに、さらに深くアルゴリズムを学び、日々のプログラミングに活用してみてください。
ここまでお読みいただきありがとうございました!
Pythonの基礎から応用まで学べる
Python WebAcademy
Python WebAcademyでは、Pythonの基礎からアーキテクチャなどの応用的な内容まで幅広く学べます。また、ブラウザ上で直接Pythonコードを試すことができ、実践的なスキルを身につけることが可能です。
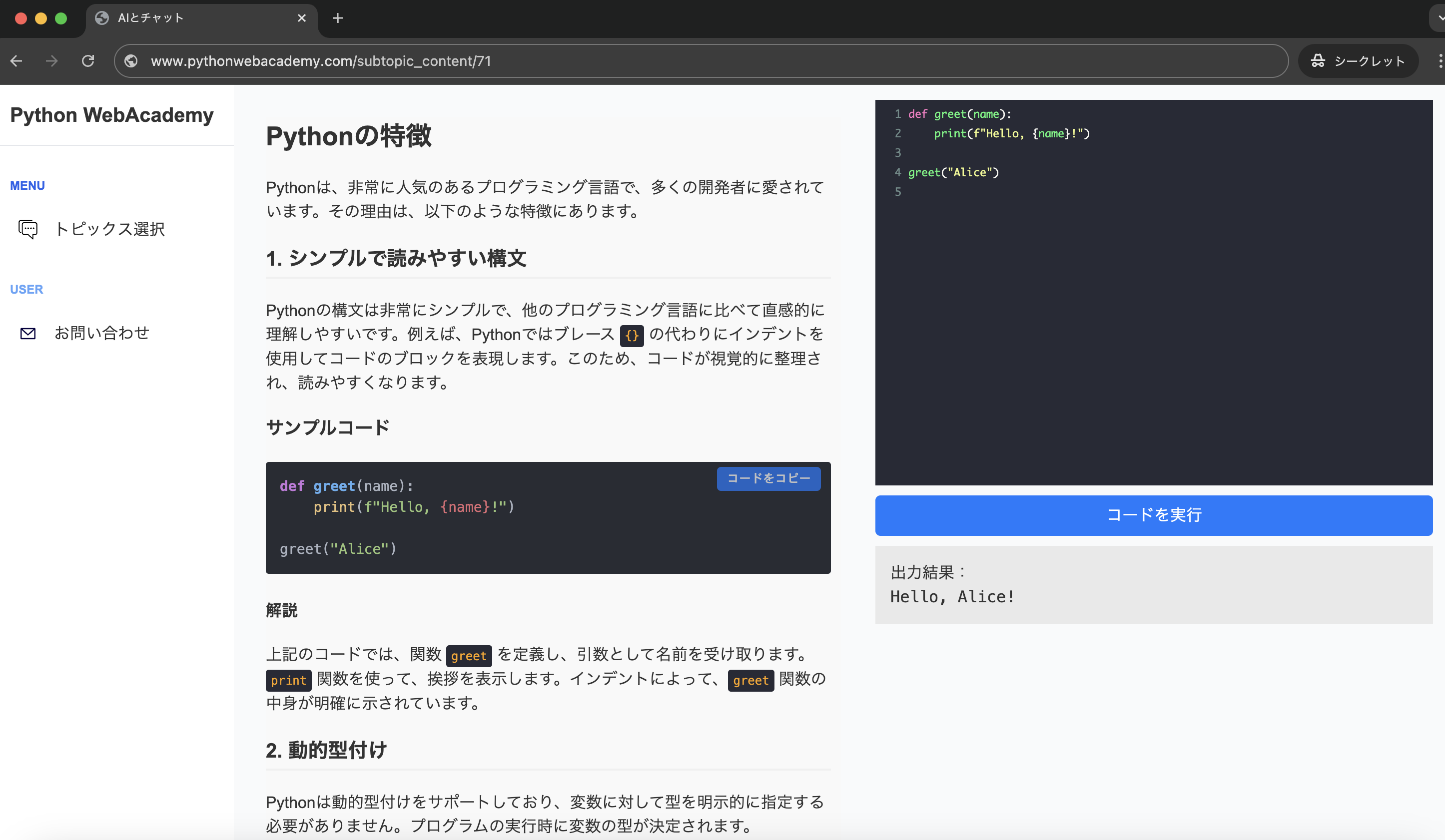 Pythonの学習を始める
Pythonの学習を始める
インフラの学習はInfraAcademy

おすすめの記事













